2015年数模研赛D题研读
问题重述
问题一:单列车运行的节能优化控制
建立计算速度距离曲线的数学模型,寻找一条列车从
A6站出发到达A7站的最节能的速度距离曲线,限定列车在两站的运行时间为110秒。建立新的计算速度距离曲线的数学模型,寻找一条列车从
A6站出发到达A8站的最节能的速度距离曲线,其中要求列车在A7站停靠45秒,限定列车在A6站到A8站的总运行时间为220秒(不包括停靠时间)。
问题二:多列车运行的节能优化控制
当100列列车以间隔\(H=\lbrace h_{1},…,h_{99} \rbrace\)从
A1站出发,追踪运行,依次经过A2,A3,……到达A14站,中间在各个车站停站最少\(D_{min}\)秒,最多\(D_{max}\)秒。间隔\(H\)各分量的变化范围是\(H_{min}\)秒至\(H_{max}\)秒。请建立优化模型并寻找使所有列车运行总能耗最低的间隔\(H\)。要求第一列列车发车时间和最后一列列车的发车时间之间的间隔为\(T_{0}\)=63900秒,且从A1站到A14站的总运行时间不变,均为2086秒(包括停站时间)。接上问,如果高峰时间(早高峰7200秒至12600秒,晚高峰43200至50400秒)发车间隔不大于2.5分钟且不小于2分钟,其余时间发车间隔不小于5分钟,每天240列。请重新为它们制定运行图和相应的速度距离曲线。
问题三:列车延误后的运行优化控制
接上问,若列车\(i\)在车站\(A_{j}\)延误\(DT_j^i\)(10秒)发车,请建立控制模型,找出在确保安全的前提下,首先使所有后续列车尽快恢复正点运行,其次恢复期间耗能最少的列车运行曲线。假设\(DT_j^i\)为随机变量,普通延误(0<\(DT_j^i\)<10s)概率为20%,严重延误(\(DT_j^i\) >10s)概率为10%(超过120秒,接近下一班,不考虑调整),无延误(\(DT_j^i\)= 0)概率为70%。若允许列车在各站到、发时间与原时间相比提前不超过10秒,根据上述统计数据,如何对第二问的控制方案进行调整?
补充说明:问题二中,列车追踪运行时,为保证安全,跟踪列车(后车)速度不能超过限制速度\(V_{limit}\),以免后车无法及时制动停车,发生追尾事故。其计算方式可简化如下:\(V_{limit}=min(V_{line},√(2LB_e))\)。其中\(V_{line}\)是列车当前位置的线路限速(单位\(km/h\)),\(L\)是当前时刻前后车之间的距离(单位\(m\)),\(B_e\)是列车制动的最大减速度(单位\(m/s^2\))。
数据与特性说明
列车参数
| 属性 | 值 |
| ————-|:————-:|
| 列车长度(单位\(m\)) | 115 |
| 列车重量(单位\(t\)) | 194.295 |
| 列车基本阻力参数\(A\)| 2.031 |
| 列车基本阻力参数\(B\)| 0.0622 |
| 列车基本阻力参数\(C\) | 0.001807 |
| 最大加速度(单位\(m/s^2\))| 1 |
| 最大减速度(单位\(m/s^2\))| 1 |
| 最小停站时间\(D_{min}\) (单位\(sec\)) | 30 |
| 最大停站时间\(D_{max}\) (单位\(sec\)) | 45 |
| 最小发车时间\(H_{min}\) (单位\(min\)) | 2 |
| 最大发车时间\(H_{max}\) (单位\(min\)) | 11 |
| 第一列列车和最后一列列车的发车间隔\(T_{0}\)(单位\(min\)) | 900 |
列车牵引和制动特性方程
最大牵引力(单位\(kN\))
\(F_{max}=\begin{cases}
203,\quad 0\leq v\leq 51.5 km/h \\
-0.002032v^3+0.4928v^2-42.13v+1343,\quad 51.5< v \leq 80km/h
\end{cases}
\)
最大制动力(单位\(kN\))
\(B_{max}=\begin{cases}
166,\quad 0\leq v\leq 77 km/h \\
0.134v^2-25.07v+1300,\quad 77< v \leq 80km/h
\end{cases}
\)
基本阻力(单位\(kN\))
\(w_{0}=(A+Bv+Cv^2)mg\)
其中\(v\)是列车当前时刻的速度,\(m\)是列车的质量,\(g\)是重力加速度。
列车动力学模型
列车在站间运行时会根据线路条件、自身列车特性、前方线路状况计算出一个限制速度。列车运行过程中不允许超过此限制速度。限制速度会周期性更新。在限制速度的约束下列车通常包含四种运行工况: 牵引、巡航、惰行和制动。
如果车站间距离较短,列车一般采用“牵引-惰行-制动”的策略运行。如果站间距离较长,列车通常会采用牵引到接近限制速度后,交替使用惰行、巡航、牵引三种工况,直至接近下一车站时采用制动进站停车。
列车在运行过程中,实际受力状态非常复杂。采用单质点模型是一种常见的简化方法。单质点模型将列车视为单质点,列车运动符合牛顿运动学定律。其受力可分为四类:重力\(G\)在轨道垂直方向上的分力与受到轨道的托力抵消,列车牵引力\(F\),列车制动力\(B\)和列车运行总阻力\(W\)。
列车牵引力F是由动力传动装置产生的、与列车运行方向相同、驱动列车运行并可由司机根据需要调节的外力。牵引力F在不同速度下存在不同的最大值,牵引力\(F\)克服阻力W和重力\(G\)做功,为了减小建模的复杂度
便于划水,我们直接忽视各站之间的坡度,这样就不用考虑重力\(G\)了呢,即只考虑牵引力\(F\)和阻力\(W\),其中\(W\)取基本阻力。由于牵引过程是个变加速过程,故在计算时我们采取无限逼近的方式,将\(\Delta t\) 内的运动看作是匀加速运动,抽象为如下过程: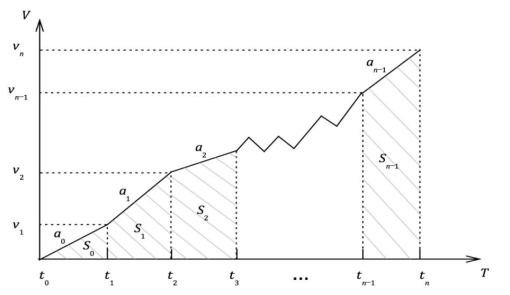
巡航阶段:列车匀速,列车所受合力为 0,列车是需要牵引还是需要制动取决于列车当时受到的总阻力
计算中把巡航这块直接无视了T_T。惰行阶段:列车既不牵引也不制动,列车运行状态取决于受到的列车总阻力,发动机不耗能。列车在速度方向只受阻力和重力的分力作用, 该过程既不产生能量也不消耗能量。由于列车车轮与轨面之间的摩擦会产生热能,从能量转化的角度来看该过程牺牲了动能。惰行过程中列车以很小的减速度不断减速。
制动阶段:列车减速,发动机不耗能。如果列车采用再生制动技术,此时可以将动能转换为电能反馈回供电系统供其他用电设备使用。由于制动过程是个变速过程,故在计算时我们采取无限逼近的方式,将每一小时间段 \(\Delta t\)内的运动看作是匀减速运动,抽象为如下过程:
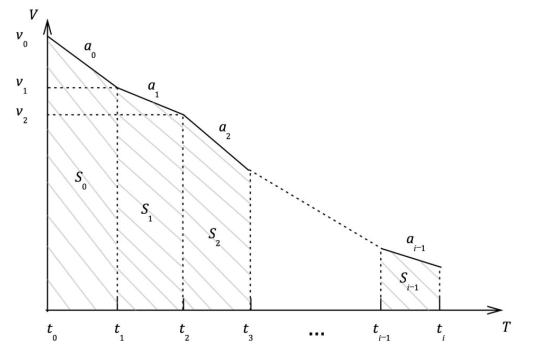
随着制动技术的进步,目前城市轨道交通普遍采用再生制动。再生制动时,牵引电动机转变为发电机工况,将列车运行的动能转换为电能,发电机产生的制动力使列车减速,此时列车向接触网反馈电能,此部分能量即为再生制动能。列车\(i+1\)在制动时会产生能量\(E_{reg}\),如果相邻列车\(i\)处于加速状态,其可以利用\(E_{reg}\),从而减少从变电站获得的能量,达到节能的目的。如果列车\(i+1\)制动时,其所处供电区段内没有其他列车加速,其产生的再生能量除用于本列车空调、照明等设备外,通常被吸收电阻转化为热能消耗掉。
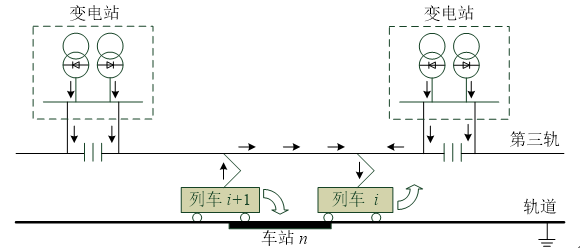
再生能量可按照以下假设的公式计算:\(E_{used}=E_{reg}∙t_{overlap}/t_{brake}\)。其中\(t_{overlap}\)是列车\(i+1\)制动的时间与列车\(i\)加速时间的重叠时间,\(t_{brake}\)是列车\(i+1\)的制动时间。即制动时所产生的再生能量与制动时间成正比。
车站线路参数
| 站点名 | 公里标 | 与下一站距离 | 限速55km/h | 限速80km/h |
|---|---|---|---|---|
| A1 | 22903 | 1334 | 120 | 1214 |
| A2 | 21569 | 1286 | 120 | 1166 |
| A3 | 20283 | 2086 | 120 | 1966 |
| A4 | 18197 | 2265 | 120 | 2145 |
| A5 | 15932 | 2338 | 120 | 2218 |
| A6 | 13594 | 1354 | 120 | 1234 |
| A7 | 12240 | 1280 | 120 | 1160 |
| A8 | 10960 | 1538 | 120 | 1418 |
| A9 | 9422 | 993 | 120 | 873 |
| A10 | 8429 | 1982 | 120 | 1862 |
| A11 | 6447 | 2336 | 120 | 2216 |
| A12 | 4081 | 1275 | 120 | 1155 |
| A13 | 2806 | 2631 | 120 | 2521 |
| A14 | 175 | - | - | - |
举例说明表中数据的含义,A6车站距离A7车站1354m,从A6车站出发前去A7车站的120m路段内列车限速55km/h,在120m至1234m路段内限速80km/h。这里特别说明一下,该表在限速路段上的数据与原题给出数据略有出入,对部分分割较为精细的路段限速值进行了粗糙的忽略,统一为限速80km/h,不影响计算结果。
单节列车节能优化
A6站至A7站
根据上述的分析,我们知道单节列车最节能的方式是:以最大的牵引力加速,然后进行惰行,接着以最大的制动力进行制动。
已知信息如下:列车参数、列车牵引和制动特性、A6站至A7站距离为1354m,运行时间为110s。按照动力学模型中三个主要过程,我们建立计算模型,取\(\Delta t=0.05s\)。列车在牵引阶段由牵引力\(F\)克服阻力\(W\)做功,列车不断加速,到达某一时间点后进入惰行阶段,列车以很小的减速度减速行驶,再到达某一时间点后进入制动阶段,准备进站停车,由此可以得知,列车在起点和终点上速度接近于0,全程的行驶速度受到列车自身限速最高80km/h和不同路段最高限速55km/h或80km/h的约束。
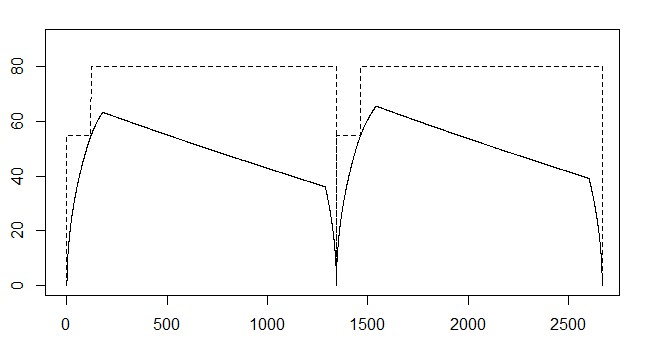
计算结果如下,实线是列车从A6站运行至A7站最节能的速度距离曲线,虚线是路段的最高限速,实线的两个拐点代表列车进入惰行和制动阶段时的距离和速度,在时间点上分别是20秒和98秒,这时列车消耗的能量约为35161kJ。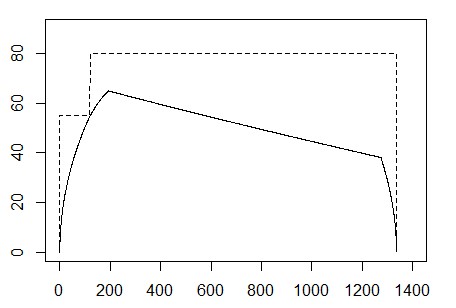
A6站至A8站
单节列车过一站和过两站的计算方法没有明显区别,可复用前一问的计算模型,要求列车从A6至A8站运行时间为220s,我们可以根据A6站至A7站的距离和A7站至A8站的距离来分配运行时间,结果如下:
| 运行路段 | 运行距离 | 运行时间 | 限速55km/h | 限速80km/h | 惰行时间点 | 制动时间点 |
|---|---|---|---|---|---|---|
| A6至A7 | 1354 | 113 | 120 | 1234 | 20 | 98 |
| A7至A8 | 1280 | 107 | 120 | 1160 | 20 | 95 |
多节列车节能优化
100列列车发车优化控制
针对单列车来说,要使得列车最节能,则采取的节能控制策略为:牵引-惰行-制动。在整体中,要使得系统最节能,则要充分利用制动产生的再生能量,故需要尽可能地延长牵引和制动的时间,使两者的时间尽可能地重叠,以便提高再生能量的利用率。
前者提到,列车追踪运行是,为保证行车安全,后车速度不仅受路段限速制约,还要考虑前后车距离限速,不过在本问中,我们分析可知:前后两列车的出发时间间隔平均约为645s,接近最大的出发间隔660s,所以在第一列列车发车时间和最后一列列车的发车时间之间间隔为63900s的限制下,列车几乎不受安全距离限速的影响。因此我们将每节列车作为独立的主题进行最节能分析,则模型回归到单节列车节能运行优化问题,我们只需求得单节列车在全路段的速度距离曲线,然后令100列列车的牵引制动时间重合度最高即可。
已知单列车A1站至A14站全路段运行总时间为2086s,为了延长牵引和制动时间,我们要尽量压缩停站时间,令停站时间为\(D_{min}\),那么我们得到全路段的实际运行时间\(t=2086-\sum_{i=2}^{13}D_{i}=1726s\),同样的,根据距离来分配运行时间,求得每个路段最节能的运行曲线,并得到惰行时间点和制动时间点,取\(\Delta t=0.05s\)。
| 运行路段 | 运行距离 | 运行时间 | 限速55km/h | 限速80km/h | 惰行时间点 | 制动时间点 |
|---|---|---|---|---|---|---|
| A1至A2 | 1334 | 101.3 | 120 | 1214 | 22 | 88 |
| A2至A3 | 1286 | 97.7 | 120 | 1166 | 22 | 84 |
| A3至A4 | 2086 | 158.4 | 120 | 1966 | 27 | 148 |
| A4至A5 | 2265 | 172.0 | 120 | 2145 | 30 | 162 |
| A5至A6 | 2338 | 177.6 | 120 | 2218 | 30 | 168 |
| A6至A7 | 1354 | 102.8 | 120 | 1234 | 21 | 90 |
| A7至A8 | 1280 | 97.2 | 120 | 1160 | 21 | 84 |
| A8至A9 | 1538 | 116.8 | 120 | 1418 | 22 | 105 |
| A9至A10 | 993 | 75.4 | 120 | 873 | 21 | 60 |
| A10至A11 | 1982 | 150.5 | 120 | 1862 | 25 | 140 |
| A11至A12 | 2366 | 179.7 | 120 | 2216 | 31 | 170 |
| A12至A13 | 1275 | 96.8 | 120 | 1155 | 22 | 83 |
| A13至A14 | 2631 | 199.8 | 120 | 2521 | 33 | 191 |
但是很惭愧,结果出了一点微小的偏差,最后一段运行速度超过了路段限速80一丢丢,查看了一下数据,最大值大约是81.37,当然选择无视他啦XD。
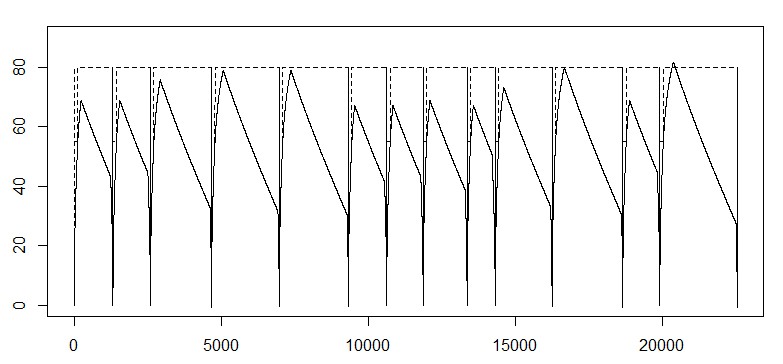
那么我们得到了单列车运行的速度距离曲线、惰行时间点和制动时间点,于是可以得到列车行进时加速和制动的时间段,其中\(T_{F}\)和\(T_{B}\)表示列车在全路段上做牵引和制动的时间集合:
\(T_{F}= \lbrace (t_{起}^{1},t_{终}^{1}), (t_{起}^{1},t_{终}^{1}),…,(t_{起}^{n},t_{终}^{n})\rbrace \)
\(T_{B}= \lbrace (\overline{t_{起}^{1}},\overline{t_{终}^{1}}), (\overline{t_{起}^{1}},\overline{t_{终}^{1}}),…,(\overline{t_{起}^{n}},\overline{t_{终}^{n}})\rbrace \)
下面考虑如何获取制造再生能最多的发车间隔,即列车之间加速和制动时间重合度最高的集合。根据我们的假设:前一列车的再生能仅供后一列车使用,那么每两列车之间的重叠时间仅仅与发车间隔有关。以第一列车发车的时间为时间零点,对不同发车间隔的牵引和制动时间段进行更新,得到:
\(T_{F}^i=T_{F}+\sum_{j=0}^{i=1}h_{j}\)
\(T_{B}^i=T_{B}+\sum_{j=0}^{i=1}h_{j}\)
\(h_{j}\)为第\(j\)列车和第\(j+1\)列车之间的发车间隔,\(T_{F}^i\)和\(T_{B}^i\)分别为第\(i\)列车做牵引和制动的时间集合。
令第\(i+1\)列车牵引加速时间和第\(i\)列车制动减速时间的重叠时间\(t_{overlap}^i = T_{F}^i \cap T_{B}^i\),则问题转换为一个令重叠时间最大的多重背包问题:有541种物品(120秒至660秒不同的发车间隔)和一个容量为63900的背包,每种物品的可用数量有一定限制,,每种物品的体积\(h_{j}\)和价值\(t_{overlap}^i\)已知,取得99件物品装入背包恰好塞满整个背包且价值总和最大,满足约束条件如下:
我们的发车间隔要求在120秒至660秒之间,这帮助我们剔除一部分位于发车间隔之外的数据。
不同的发车间隔对应的列车车数之和应该等于99,并且他们的乘积之和等于63900秒。
我们要求在限定时间63900秒完成全部100列车在全路段的运行,这样一来即使取平均值,发车间隔也在640秒左右,这帮助我们剔除一部分距离均值较远的数据,一来简化我们的计算,二来确保结果的可靠性。
要求发车间隔序列下重叠时间最大,这样得到可利用的再生能最多,使得总耗能最小。
这样,我们实际上从541种物品(120秒至660秒不同的发车间隔)筛选出平均值上下的数据(620秒至660秒),即有41种物品。最后设计的算法一个没有控制不同发车间隔对应列车车数之和为99的粗糙算法计算结果显示出一个趋势,我们总是得到两个不同的发车间隔,他们对应的列车车数接近,且和靠近99,这意味着什么呢,意味着该模型的最优解可能是两个不同的发车间隔,他们对应的列车车数相差不大,且满足第二个约束条件,按照这一思路骚断腿的反向操作,我们直接可以得到最优解为50列发车间隔为641秒,49列发车间隔为650秒,计算重叠时间是3161秒,有种强行凑答案的感觉。
余下的问题
待续GG。
总结
看了别人的论文感觉真的强啊,看了自己的操作真的头疼,怕是成功参赛奖预定了,不过还是要挣扎一下的,毕竟生命在于折腾。
如何联系我?
不如就用邮件吧,请戳左上角。
最后
感谢阅读完这段内容,谢谢,祝您生活愉快,have a nice day ~
彩蛋
Youtube上有一个挪威地区列车行进的直播,可以欣赏挪威这个国家沿途的风景
替换为一个相关的视频吧,亦可自行搜索,关键词是train view。
参考资料
赵丹玲, 程然, 杨风波. 面向节能的单/多列车优化控制研究